Faraday’s Flux Rule – Joseph Henry Project

Ryan Hunstein

2023

Research Questions:

What is Faraday’s Paradox?
What is the relationship between induced EMF, Faraday’s Flux Rule, and the Lorentz Force Law?
Does centripetal force induce an EMF in a rotating copper disk without a magnetic field present?

What is Faraday’s Paradox?

Faraday’s Paradox is a phenomenon in which Faraday’s Flux Rule predicts zero EMF where the EMF is nonzero experimentally.

Example: Unipolar Generator

Left: A 1930 model of Faraday’s original 1831 unipolar generator from the National Museum of American History, deemed the “Faraday Disk.”

Right: A collection of diagrams depicting the early unipolar generator from Volume I of Faraday’s Experimental Researches in Electricity.

In the unipolar generator, a conducting disk rotates symmetrically about its axis in the presence of a magnetic field perpendicular to its face. Upon connecting a multimeter to the center axle and stationary brush against the rotating perimeter, an EMF is detected. Since there is no changing magnetic flux in this problem as magnetic field and area remain constant, zero EMF is expected. So, upon first glance, this scenario is paradoxical.

Solving the Paradox

In reality, the phrase “paradox” is a misnomer since this phenomenon is not a scientifically self-contradictory statement. Rather, it appears paradoxical under the current understanding of Faraday’s Flux Rule when only using . In fact, this “paradox” brings attention to the importance of the Lorentz Force Equation .

To derive the complete EMF induction equation, Maxwell’s Equation and the Lorentz Force Equation are to be used. The below follows Crooks et al. 1978.

W = qε =
ε =
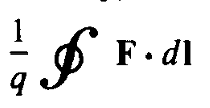
Substituting the Lorentz Force Equation, ε =
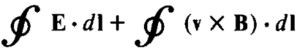
Using Stokes’ Theorem, ε =
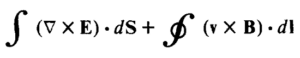
Substituting Maxwell’s Equation, ε =
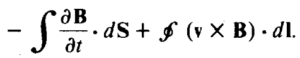
When moving the partial derivative outside the integral, it becomes a full derivative since the integrand only depends on t. ε = +
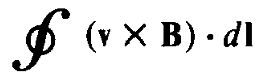
Rewriting, this yields ε = +
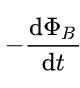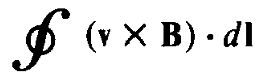
This can be written as ε = ε flux + ε motional

It is important to understand that Faraday’s Flux Rule is a good generalization of induced EMF in certain situations, but fails to account for the entire picture in more particular ones, such as the unipolar generator. Now, using this new and complete form of an equation for EMF induction, we can take another look at the unipolar generator.

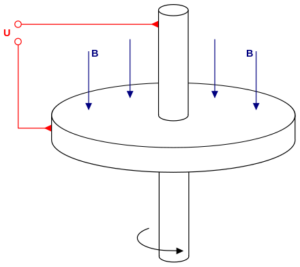
There is no changing magnetic flux since the area and magnetic field remain constant, so equation 7 becomes simplified to V = where v is the velocity of the conductor. Here, the tangential velocity of the conductor as it rotates with angular velocity w is given by v = w r where r is the radius of the copper disk. This velocity points tangentially counterclockwise from a top-down view. This is perpendicular to the magnetic field pointing into the page, so a nonzero EMF is induced. Applying the Right Hand Rule, the voltage is induced radially inwards everywhere on the disk. This is the voltage detected by the multimeter.

NOTE: Since velocity is larger on the outer radius of the disk, there is more force exerted on the charges near the rim of the conductor than closer to the center. This theorizes that the charge separation is greater on the outer rim of the conductor.

Centripetal Force

Continuing with EMF being induced by the Lorentz Force Law, thoughts of what other forces could be involved to induce EMF come to mind. In particular with the case of the rotating copper disk a centripetal force is known to be present on mass points outside the center.

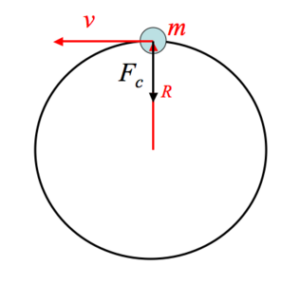
Because of this, it is believed that a nonzero EMF would be induced radially inwards in the case of a rotating copper disk, even if there is no external magnetic field present! Of course, this force will usually be negligible since it depends on the very small mass of the electrons.

Since F = and ε =, this yields ε =

Conclusion

In summary, Faraday’s Flux Rule written in common form is incomplete and yields a paradox as seen with the unipolar generator. However, when deriving the EMF induction equation from the Lorentz Force Equation, it is more complete. It accounts for both the EMF induced from changing magnetic flux and motion of the conductor. Additionally, centripetal force plays a negligible yet existent role in inducing an EMF mechanically without the presence of a magnetic field. This suggests that the entire, true form of the law is:

ε = ++