Exp. 8
Experiment 8
1 60 ft Coil – Lifted 7 lbs
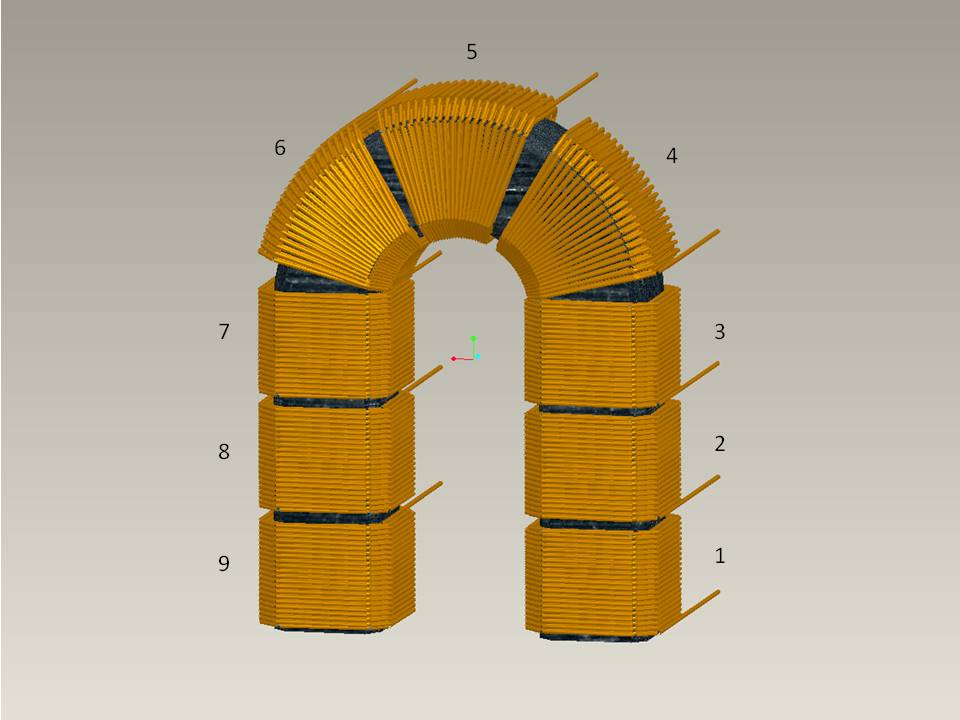
Henry connects each coil (1-9) to the battery one by one. He finds that each coil by itself is only able to lift the armature, which ways only 7 pounds.
Exp. 9
Experiment 9
2 60ft Coils in parallel – Lifted 145 lbs
When coils 4 and 6 are both connected to the battery, the lifting power is greatly increased, almost 21 times the lifting force of the last experiment. How could this be? From equation 7 we know that the lifting force is proportional to $B^2$, however that would indicate a maximum lifting force of about 49 lbs. There is something missing. Something seems to be limiting the lifting power of the magnet in experiment 8. We can explore several factors that may or may not have contributed to this: 1) Even though the material he used was “soft iron,” one possible explanation for these contradicting results could be some residual magnetism that could have been developed during the forging process. All iron has some type of impurities in it. A likely iron that Henry would have used is Wrought Iron, which is high purity but still has some carbon impurity in it. Any amount of carbon can result in some sort of residual magnetism. When iron is heated and worked, it can develop its own magnetism. If Henry was connecting the coils in experiment 8 opposite to the residual magnetism, it may have resulted in a decrease in lifting strength. 2) It could be that the battery was acting differently under a smaller load. His galvanic cell could allow for less current to be drawn when only one coil is attached. 3) In the hysteresis curve of iron, the very first increases of magnetic field strength causes a short exponential increase in the B-Field. A exponentially increasing B-field could make the lifting force increase rapidly. 4) Because the magnet was only lifting the armature in experiment 8, the net force on the magnet poles was small. The contact between the armature and the horseshoe’s poles may not have been completely smoothed out until a greater net force was acted upon the armature (another coil was added). If a greater net force was able to produce a smoother contact, this would mean a smaller air-gap, which would result in an overall larger lifting force.
Some of these ideas are more plausible than others, but it is still uncertain which one(s), if any, gave these contradicting results.
Exp. 10
Experiment 10
2 60 ft Coils in parallel – Lifted 200 lbs
When coils 1 and 9 are both connected to the battery, there is a significant increase in force over the last experiment. Here the magnetic field strength should be the same, however, the flux density at the point of contact increases. This is due to the fact that the both coils are very close to the point of contact, minimizing flux leakage due to magnetic reluctance (equation 9) at that point. Placing the coils close to the point of contact focus more magnetic field lines through the point of contact, thereby increasing the flux density and lifting power at that point. Because there is a certain theoretical reluctance associated with the entire magnetic circuit, there is a certain amount of flux that should flow though the entire circuit. Consequently, the loss of flux from reluctance into the air occurs primarily away form the point of contact, which provides a better lifting strength than if the coils were wound completely around the entire magnet – or a totally uniform leakage.
Exp. 11
Experiment 11
3 60 ft Coils in parallel – Lifted 300 lbs
When coils 1, 5, and 9 are all connected to the battery, there is a substantial increase of lifting power due to an increase in the magnetic field strength (increasing the of Ampere-Turns). Here the magnetic fields lines slightly less focused at the polls than the last experiment because of the increase in uniformity of the leakage. Because of the significant increase in lifting force, the battery or iron seem to show very little signs of saturating.
Exp. 12
Experiment 12
4 60ft Coils in parallel – Lifted 500 lbs
When coils 1, 2, 8, and 9 are all connected to the battery, there is a an even greater increase in lifting power over the last experiment. This difference can be explained much like experiment 10, by an increase in flux density at the poles of the magnet due to the location of the coils being near the poles.
Exp. 13
Experiment 13
6 60ft Coils in parallel – Lifted 570 lbs
When 6 coils are connected to the battery (Henry does not mention the location of coils in this experiment), we can see that the increase in lifting force has suddenly diminished significantly. This is most likely caused by three reasons: 1) The flux leakage is almost completely uniform, decreasing the density of flux at the poles compared to the last experiment. 2) The resistance of the cell is nearing the resistance of the load (the equivalent resistance of all the coils in parallel), diminishing the amount of current being drawn. 3) It is possible that the soft iron core is quickly reaching nearing its saturation, thereby decreasing the value of $mu$ in equation, which also increasing the reluctance, causing a larger amount of flux leakage.
Exp. 14
Experiment 14
9 60ft Coils in parallel – Lifted 650 lbs
When all 9 coils are connected to the battery, we see that Henry gets a very similar increase in lifting force. Since the battery and/or material have begun to saturate, we would expect to see a larger decrease in performance. However, with addition of coils we see almost the same increases as the last experiment. This is due to the flux being almost as uniform as the experiment before. Experiment 13’s force increase diminishes dis-proportionally to experiment 12 because of a significantly different coil configuration.
Experiment 15
9 60 ft Coils in parallel – Lifted 750 lbs
When all 9 coils are connected to a larger battery composed of a single galvanic element with a plate of zinc 12in x 6in surrounded by copper, the lifting force increases. This is due to a decrease of the internal resistance of the battery, allowing even more current to flow through the coils. After the experiment Henry mentions that the magnet is “probably, therefore, the most powerful magnet ever constructed.” Henry notes that with a large calorimeter, containing 28 plates of copper and zinc each 8 inches square, he could not succeed in making it lift as much weight as with the small battery. This is due to the fact that a battery that large will have a very high internal resistance (the sum of each cell’s resistance). As discussed before, when the source resistance is much far greater than the load resistance, the addition of coils in parallel will not draw any significant additional current to increase the magnetic field strength. Only adding coils in series will noticeably increase the strength of the magnet. Henry tests this hypothesis later in these experiments.
Experiment 16
1 60 ft Coil – Lifted 85 lbs
To see the effect of using a very small amount of zinc and copper, Henry substitutes a very small galvanic element with a pair of plates 1 inch square was substituted for the last element. With all the coils connected, the magnet only lifts 85 pounds. We can see that by decreasing the area of zinc and copper, the internal resistance of the battery increases a significant amount, limiting the current flow.
Experiment 17
6 30 ft Coils in parallel – Lifted 375 lbs
Henry attaches 6 30 foot coils, presumably cutting 3 60 ft coils in half. This increase over experiment 11 is simple. Decreasing the resistance of each coil allows for more current to flow, keeping with the assumption that the source resistance is still very low. This increased magnetic effect due to higher current is somewhat camouflaged due to the increase in uniformity of flux in the magnetic circuit (assuming all the coils were connected along the circuit and not on top of each other), but is still obviously significant.
Experiment 18
3 60 ft Coils in parallel – Lifted 290 lbs
Henry unites the 6 30 ft coils to form 3 60 ft coils and attaches them much like experiment 11. The results are indeed very similar to experiment 11 (300 lbs). Henry notes that the 6 shorter wires were more powerful than 3 of double the length. Again, this is due to the ability of 6 smaller coils to draw a larger amount of current. We still do not know however what locations these coils were connected.
Experiment 19
1 120 ft Coil – Lifted 60 lbs
Henry Unites the 2 60 ft coils from experiment 10 (200 lbs) to form 1 120 ft coil. This simply allows for less current to be drawn, decreasing the magnetic field strength. This also confirms the assumption that when only 2 60 ft coils are connected in parallel to the battery, the equivalent resistance of the load is still greater than the source.
Experiment 20
1 120 ft Coil – Lifted 110 lbs
When Henry attaches the same long coil to a small compound battery, consisting of two plates of zinc and two of copper, containing the same quantity of zinc surface as the element in the last experiment, the lifting strength almost doubles. Henry calls this configuration to have more “projectile force, and thus producing a greater effect with a long wire.” By combining 2 cells in series, we understand the effect created as increases of voltage, and resistance. As mentioned earlier, a source with a higher resistance is greater suited with a load with similar resistance. Here Henry was simply attempting to match resistances to maximize the lifting strength with a finite amount of turns.