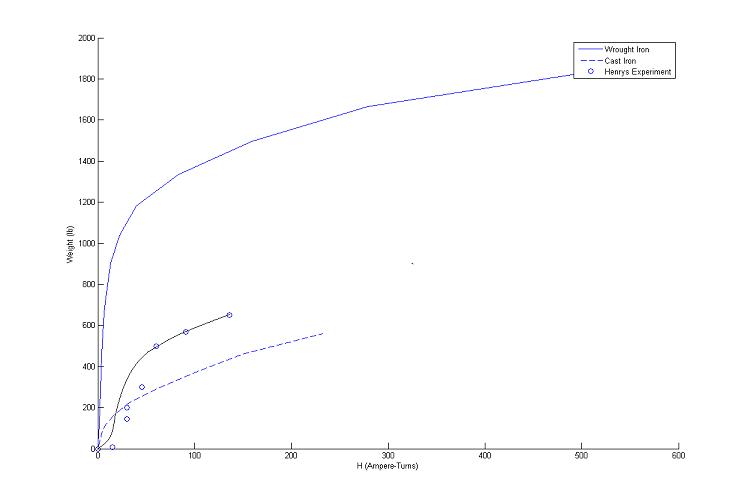
Data Analysis – Theoretical Comparison
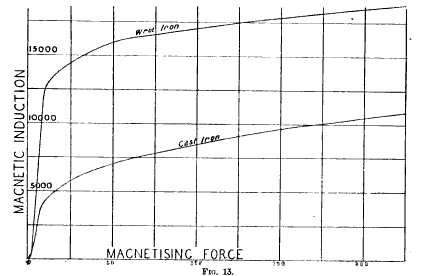
The experimental data (exp 8 – 14) shows an exponential shape before saturating and leveling off. This can be compared to the a theoretical saturation of both wrought and cast iron in the figure above. As shown, the material Henry used was somewhere between The value of H for Henry’s data depends on the amount of current drawn from the galvanic cell, which depends on a currently unknown value of internal resistance. However, we estimate the resistance of his single galvanic cell to be fairly high, somewhere around 5 ohms. The first 4 points on the graph are offset from the fit line, showing the diminishing loss of magnetic flux density due to the leakage of magnetic force lines.
(The Electrical Engineer, Vol.11 (July 1893): pp.95,173)
The following MATLAB syntax was used to construct this comparison.
hold on
H1=[0,1.66,4,5,6.5,8.5,12,17,28.5,50,105,200,350,660]./(4.*pi./10);%Magnetomotive force in ampere-turns
B1=[0,5000,9000,10000,11000,12000,13000,14000,15000,16000,17000,18000,19000,20000].*(.0001); %Flux Density is Tesla
F1=(((2.*(B1.^2).*(4.*(.0254.^2)))./(2.*u0))).*0.224808943; %Force in Pounds
p1=plot(H1,F1,’-‘);
H2=[0,5,10,21.5,42,80,127,188,292]./(4.*pi./10);
B2=[0,4000,5000,6000,7000,8000,9000,10000,11000].*(.0001);
F2=(((2.*(B2.^2).*(4.*(.0254.^2)))./(2.*u0))).*0.224808943;
p2=plot(H2,F2,’–‘);
coils=[0,1,2,2,3,4,6,9]; %Data from Joseph Henry’s Paper
weight=[0,7,145,200,300,500,570,650];
d=.045*(.0254); %Diameter of the wire used in meters
A=pi*(d/2)^2; %Cross sectional area of the wire used
L_c=60*12*(.0254); %Length of wire used in each coil in meters
ro=1.68*10^-8; %Resistivity in ohm-m
R_L=ro*L_c/A; %Resistance of each coil
R_S=5; %Resistance of the galvanic cell, assuming the batteries
%he used had fairly high resistance compared to modern batteries.
R=R_L+R_S; %Total Resistance of Circuit
I=(1/(R)); %Current in each coil
N=coils.*80; %Number of turns
H=((I.*N)); %Magnetomotive force in ampere-turns
p3=plot(H,weight,’o’)
xlabel(‘H (Ampere-Turns)’)
ylabel(‘Weight (lb)’)
legend([p1,p2,p3],’Wrought Iron’,’Cast Iron’,’Henrys Experiment’,1)