Ryan Yu | 6/14/2025
Background
In the early 19th century, electricity and magnetism were subjects of growing scientific interest, but they were mostly studied separately. This changed in April 1820, when Danish physicist Hans Christian Ørsted made a groundbreaking discovery: an electric current flowing through a wire could deflect a nearby compass needle, revealing a direct connection between energy and magnetism.
No one investigated this phenomenon as fervently as French physicist André-Marie Ampère, who began to experiment with electric currents and magnets himself in a Paris laboratory:
“I have been seeking to express the value of the attractive or repelling force between two elements, or infinitesimal parts, of conducting wires by a formula so as to be able to derive by the known methods of integration, the action which takes place between two portions of conductors of a given form and position; for it is evident that the interaction does not depend solely on distance” (Letter to Francois Arago, 1820)
Less than a year later in January 1821, Ampère published his findings in the Annales de Chimie et de Physique, France’s premier scientific journal. Ampère conducted the two-wire experiment, in which electric currents flow through two parallel wires. He observed that the wires attracted each other when the currents flowed in the same direction–evidence that electric currents produce magnetic effects, and current-carrying wires behave like magnets.
From this he deduced, “If all the elements [magnetic field] on a particular surface are of equal intensity on equal areas, they can be replaced by a single current flowing along the curve formed by the intersection of this surface and that of the magnet.”(Annales De Chimie et de Physique, Vol. 18. 1821. Page 90).
He would go on to mathematically prove a mathematical relationship between electricity and magnetism, unifying the two fields. He states in 1826:
“if magnets only owe their properties to electric currents, which encircle each of their particles, it is necessary, in order to draw definite conclusions as to the action of the conducting wire on these currents, to be sure that these currents are of the same intensity near to the surface of the magnet as within it” (Mathematical Theory of Electrodynamic Phenomena, Uniquely Derived from Experiments, Page 4)
This page documents a recreation of the two-wire experiment in COMSOL that confirms Ampere’s original observations and hypotheses.
A brief overview of Ampere’s Law
Ampère’s Law describes the relationship between electric currents and the magnetic fields they produce. In its integral form, the law states that the line integral of the magnetic field B around a closed loop is proportional to the total current I passing through the loop. Ampere observed this principle by running currents through two parallel wires, discovering that they exerted forces on one another, just like magnets do.

COMSOL Setup
Two parallel conductors, each a 1 mm radius copper wire, are spaced 5 mm apart. When a current of 1 ampere flows through both wires in the same direction, the wires attract each other due to magnetic interaction. The 1st visualization shows the direction and magnitude of the magnetic flux density, illustrated with color scale and blue streamline, respectively. The red streamlines show the direction of the current flow.
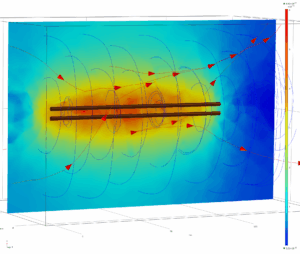
The attractive force exerted by the magnetic field of the top wire acting on the bottom wire is also confirmed with an arrow plot of Lorentz Force density (see later)
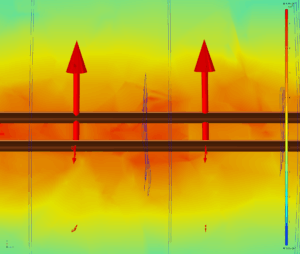
Conversely, when current flows in opposite directions, the bottom wire feels a net repellent force:
*Future calculations assume a setup with current flowing in opposite directions
With these observations in hand, I proceed to prove Ampere’s hypothesis in 1826:
“If magnets only owe their properties to electric currents, which encircle each of their particles, it is necessary, in order to draw definite conclusions as to the action of the conducting wire on these currents, to be sure that these currents are of the same intensity near to the surface of the magnet as within it”
Two calculations are made to calculate the “surface intensity” and the “intensity within” one wire in COMSOL, each described below:
Maxwell Stress Tensor Method: Integrating the Maxwell stress tensor over the surface of the wire, essentially performing a clean surface integral of the electromagnetic forces exerted on the wire to obtain the “surface intensity”.

(T multiplied by n is the normal vector of the stress acting to the surface, integrated across the continuous surface area of the wire)
Volumetric Lorentz Force Method: Integrating the Lorentz force density (J*B) over the wire’s volume to obtain the “intensity within”

J, the current density, multiplied by B, the magnetic density gives the Force per unit volume perpendicular.
Simply put, Ampere observes that if “all the elements of a particular surface are of equal intensity on equal areas, they can be replaced by a single current flowing along the curve formed by the intersection of this surface and that of the magnet.”
Essentially, adding up the magnetic strength on the surface of the wire should equal the amount of electric current flowing inside the wire. Confirming that the magnetic field calculated outside the wire matches the current inside confirms Ampere’s observation, deduction, and law.
Below are the obtained force values measured by the electromagnetic force exerted on each wire by the other’s magnetic field, when 1 amp flows through each wire (in the case when current flows in opposite directions):
Maxwell Stress Tensor: -3.57e-6 (repellence) 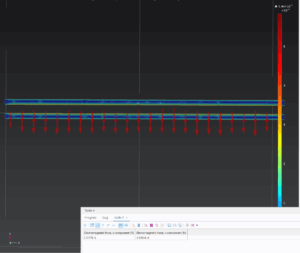
Lorentz Force Density: 3.03e-6 
As Ampere predicted, these values are very nearly the same.
Arrow plots of the Maxwell Stress Tensor and the Lorentz Force Density on the cross section (In the case of currents of 1[A] flowing in opposite directions):
Maxwell Stress Tensor: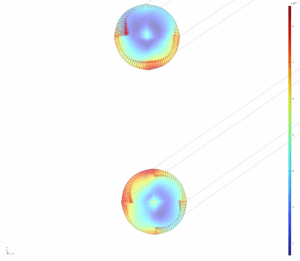
Lorentz Force Density: 
Notice how the Maxwell stress tensor points are distributed around the whole boundary, and the Lorentz Force Density shows an inwards pointing force where the current interacts with the magnetic field!
Ampere would continue his investigation by examining magnetic fields in more shapes, including in solenoids and single wires. Click here to see some more magnetic field visualizations!
Outside resources:
Ampere’s Correspondence to Faraday Archive
Foundations of Electrodynamics