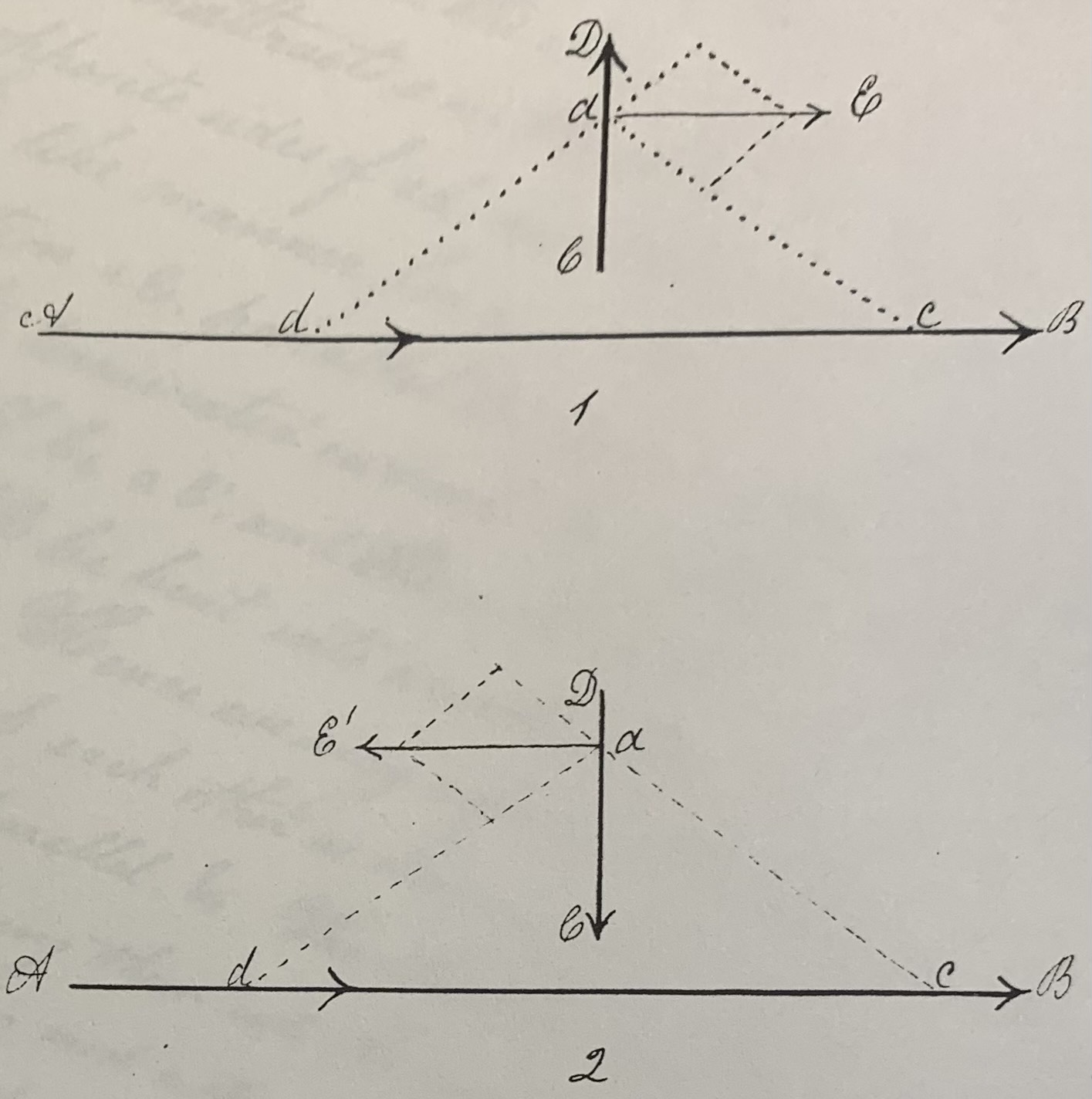
In his lectures, Joseph Henry tests electromagnetic theories through models and experimentation for his students. His experimentations are detailed in the notes of Henry C. Cameron, a teaching assistant of Henry. Henry begins Lecture 59 by recalling Coulomb’s Law. He uses a diagram of currents (fig. 1,2) to demonstrate that attraction and repulsion between two electrically charged elements is the inverse of the square of the distance. For example, at distance d, the current c will have a certain effect upon the element. At twice this distance, it will only have ¼ the effect. The intensity of the action is also the inverse of the distance. For example if the current is twice as long, the whole effect will be one-half as great; at three times the distance, one thirds. Henry proved this by experiment as the intensities of the forces were ascertained by referring to the number of oscillations performed by the needle in a given time, and taking the square of those measurements.
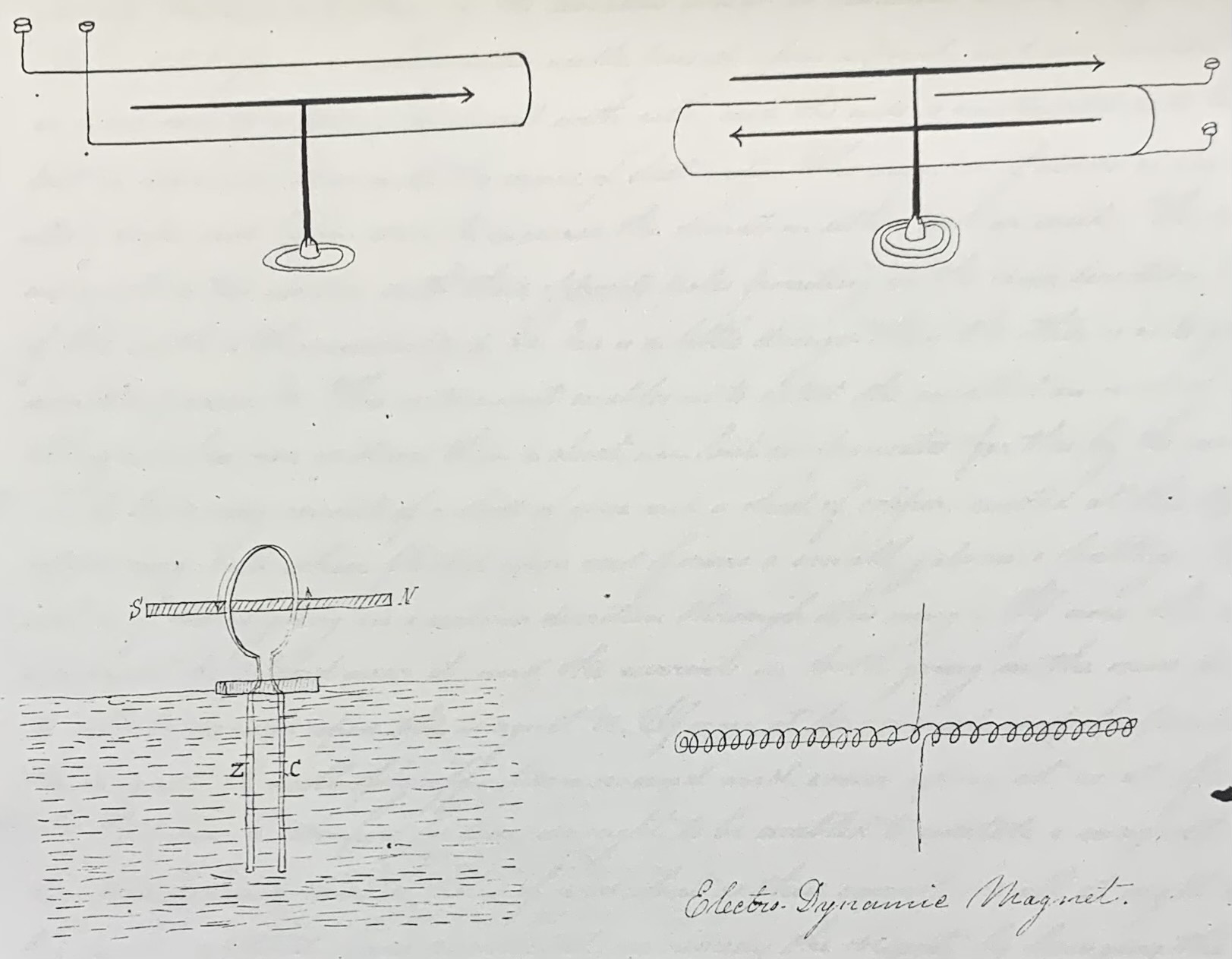
The lecture then shifts to Ampere’s theory. Henry explains that when a magnetic needle that is not influenced by Earth’s poles is placed under or above a current carrying wire, the needle will align itself perpendicular to the wire. According to Ampere, this and all magnetic attraction is all a result of electric currents. The Galvanometer, De La Rive’s ring, and Ampere’s frame are all examples of this that Henry discusses.
The Galvanometer consists of a magnetic needle surrounded by copper coils of wire that extend so as they can be connected to a potential source of electricity. If the wires come in contact with an electricity source, they will conduct a current which will create a magnetic field causing the magnetic needle to move based on the strength of the electric current and subsequent magnetic field. This property allows electrical currents to be measured.
This phenomenon is also seen in De La Rive’s ring. The ring consists of a galvanic battery floating in acid with a copper ring attached on top. The charge from the battery creates a current through the copper wire and subsequently a magnetic field. The ring can then be attracted or repelled with other magnets or can align to Earth’s poles just as a common magnet. This further proves Ampere’s theory that magnets are solely driven by electrical currents. Joseph Henry used a physical model and detailed diagrams to teach this (fig. 3)
Ampere’s frame is made up of a current conducting wire with one end dipped into a small cup of mercury with a horseshoe magnet below. When electricity flows through the wire, it rotates in oscillation. If a copper disc were to be placed underneath, the wire would dampen and eventually settle where it is perpendicular to the magnet. Joseph Henry used a physical model of Ampere’s frames and illustrations to demonstrate this (fig 1,2).
Original Transcription:
A theory is an expression for the law which forwards a class of phenomena and the use of it is that we have something to which we can refer facts ie. enclaim the and from which also we can make deductions, If the theory be true, and the deduction be strictly logical, the experiment must be such as you had predicted. This theory of Ampere, as was stated in the preceding lecture, serves to obtain many phenomena, and has led to the discovery of many facts. We may show by experiment that currents in the same way attract, and in opposite repel. We increase the effect by sending the currents through coils of wire. If the poles of a battery be in connection with one coil of wire, and another coil be placed parallel to it, and in connection with another battery, the two coils will attract if the currents be going through both in the same direction; and repel if in opposite. This attraction and repulsion takes place through non-conductors, as well as conductors, just like electricity. The attraction and repulsion is inversely as the square of the distance, and directly as the product of the number of the elements of the currents. By element we xxx of the whole current. From a clean physical analogy we infer the first part of this proposition. But in the magnet we may regard the action as xxx in the poles, whilst in the conducting wire, the fluid acts in an equal degree along the whole line of motion, hence we must deduce a law which will be the result of the combined action of all the points in a line upon one without it. We will confine the effect within the lines AB and AC. At the distance d, the current c will have a certain effect upon the element dc. At twice the distance, it will only have ¼ the effect, but the current is twice as long, and therefore the whole effect will be one-half as great; at three times the distance, one thirds Hence the intensity of the action will be inversely as the simple distance, This has been proved by experiment. The intensities of the forces were ascertained by referring the number of oscillations performed by the needle in a given time, and taking the square of those numbers.
We would at first suppose that when a current of indefinite length acted upon a short terminated one at right angles to it, there would be no effect. This however is not the case. If the indefinite current be going in the direction AB, and the terminated one in the direction CD at right angles to the former, yet the influence of the element c upon the element a, is not thus; but both moving on the same side of ac. d repels a in the direction ad, being on the opposite sides of ad; and the resultant of these two forces is the direction aE parallel to itself and always keeping perpendicular to AB. If now the terminated current be xxx in the direction DC, the resultant as above will be aE’ and xxx will move as before only in an opposite direction. If now AB be bent into a circle, there must result a rotary motion parallel to it. So hence we may explain the rotary motion in yesterday’s lecture. If currents cross each other as shown in fig 3,4, and 5, they will tend, if left free to move, to come parallel. The attractions are represented by +, the repulsions by -, and both conspire to bring them into the same plane, as seen by the figures , there are four forces. The action of a circular and a straight current is such as exhibited in figure 6. In the parallelogram the upper nearly neutralizes the lower, and the side currents both conspire to turn it into the same plane. So with circular current, those at the sides
It has been shown before that when a current is xxx over a magnetic needle, and the action of the earth is neutralized, it stands at right angles to the wire. The explanation of this according to Amperes theory, is that the currents around the needle tend to coincide in direction with that in the wire. The currents around the inner atoms are supposed to neutralize one another, and only the interior ones to act. Then currents may extend into space.
According to the theory of Ampere there is no such thing as magnetic attraction and repulsion. It is all due to the action of currents of electricity.
The Galvanometer is an instrument for ascertaining the presence of a current of electricity especially Galvanic or Voltaic, by the deviation which it xxx in the magnetic needle The simplest form is a horizontal needle raised from a joint and surrounded by one or more coils of copper wire covered with xxx, and the ends so constructed as to be easily xxx in communication with he source of electricity. The number of wires, as also their position above and below serve to increase the deviation either east or west. The compound one exists on two needles with their opposite poles pointing in the same direction. The action of the earth is thus neutralized. One is a little stronger than the other so as to give a little directive power. This instrument enables us to detect the smallest amount of electricity A long wire has more resistance than a short one but compensates for this by the number of xxx De La Rive’s ring consists of a sheet of zinc and a sheet of copper, united at the top by a copper ring, and when floated upon acid forms a small galvanic battery. The current is of course going in a certain direction through this ring. If now the end of a magnet be placed near it, amid the currents in both going in the same direction, it will be drawn upon the magnet . If now it be reversed, and be pushed upon the magnet, it will fly off, turn round and come upon it as at first. If the theory of Ampere be true, we ought to be enabled to imitate a magnet. We therefore form a spire or xxx of wire; but as these cannot be all at right angles to the length without being disconnected, we remedy the obliquity by bringing the wire back upon itself. Of this be now suspended, and a a current of electricity be sent through it, it will manifest directive property just as a common magnet, though in a less degree. It will be attracted and repelled by the common magnet.
Two galvanic magnets attract and repel each other precisely as common magnets as may be shown by experiment. Also the revolution produced by galvanic magnets is the same as that by common magnets. Thus affording a proof of the truth of what appears to be the xxx theory of Ampere.
If a wire be suspended with its lower end in mercury, and between the poles of a horse shoe magnet lying flat, and a current of electricity be sent through the wire by means of a communication with source of electricity above, and through the mercury below, it will of course tend to revolve around each pole of the magnet. Hence a vibratory motion would ensue, the wire would be thrown out, the communication would then be broken, it would fall back; and the same action would again take place. So also a wheel which may be considered as made up of an infinite number of radii, each of which is thrown out in succession, may be thus made to revolve with great rapidity.
If a magnet be fixed perpendicularly in a cup, and have its lower and have its lower half imbedded in mercury, and its ends so fixed that it will be at liberty to revolve; by sending a current of electricity through the upper half it may be made to revolve with great rapidity. Xxx arrangements have also been made for causing the revolution of a magnet on its own axis by means of currents. If the electricity be very intense, we use a very long wire. The resistance of a wire is directly as its length and inversely as its sectional area. There is a certain length of wire which will produce the maximum effect. This must be determined by experiment, combined with the laws in regard to resistance.
It is a remarkable fact that the intense electricity from an electrical machine does not affect the galvanometer. If however it be sent through xxx long wire, and then through a wet string, we may affect the galvanometer by xxx.
If we place a piece of zinc not more than a inch long, and one nineteenth of an inch in diameter, with a piece of copper of the same size, into sulphuric acid, and connect them with the galvanometer, it is immediately affected; a greater quantity of electricity being generated by them, than by the machine. They give it off by atoms, it by sparks. The whole amount given off by these in half an hour or during their dissolution is sufficient to charge a thunder cloud, so much electricity is there combined with metals.