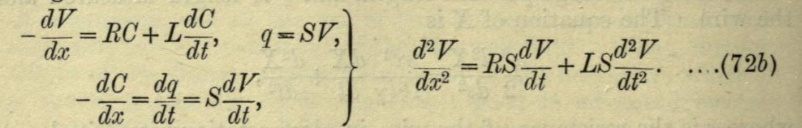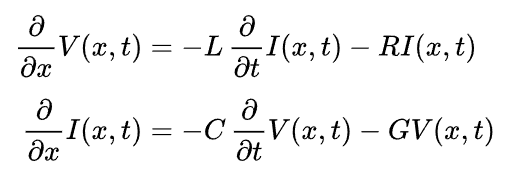Though many associate Oliver Heaviside (Learn more about him here) with the formulation of the Telegrapher’s Equation in 1876, the first steps to developing transmission line theory had already been taken by William Thomson, otherwise known as Lord Kelvin. He first proposed the idea of the lumped element model, stating ‘the quantity of electricity on a length dx of wire … will be v*c*dx,” and also formulated that signal propagation through transmission lines behaved very similarly to the dispersion of heat in the heat equation meaning that he could simply use the solution already derived by Fourier (using Fourier series to model any function as a sum of sine functions, which were solutions to the wave equation and simply over time attenuated to a factor of itself) to model the propagation voltage and current of telegraph signals. 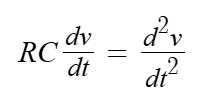
Additionally, using Fourier’s solution, he formulated higher frequency signals would attenuate faster, and that the time delay is proportional to K*C*L2, where K is resistance, C is capacitance and L is the length of the cable. This means “the time required for each deflection will be sixteen times as long as would be with a wire a quarter of the length.” To combat this, Thomson proposed a larger cable to have a lower resistance and capacitance, but in the case of the first transatlantic telegraph cable in 1858, was largely ignored, instead opting for Whitehouse’s recommendation of a thinner cable. Notably the first Transatlantic was a bunch of 7 wound copper wires, insulated by gutta percha, a natural latex, widely used in the 19th century made from the sap of the Palaquium Gutta tree and weight 550kg/m. This led to much longer transmission times (over 17 hours for Queen Victoria’s initial transmission). Additionally, following Whitehouse’s recommendations, who did not believe in Thomson’s theory, sent over 2000V through the cable, destroying it indefinitely. The next cable in 1866 followed Thomson’s recommendations and following its success, Thomson was knighted to become Lord Kelvin.
Heaviside’s contribution however, added onto Kelvin’s work by including the idea of inductance, with a proportional voltage drop along the line not only proportional to the rate of change of the charge, but also the rate of change of the current.
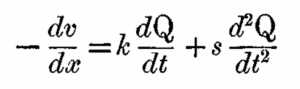
While Thomson introduced the idea of diffusion, Heaviside introduced the ideas of wave dispersion. By doing so, he noticed the “extra current” caused by the inductance of the transmission line, hence the name of his paper.
Solution of lossy telegraphers' equation with dispersion vs lossless wave-equation, modified from here View the Mathematica code here
Here you can see the equations written out by Heaviside in his Electrical Papers, and the modern format of the equations. Note the RLGC parameters can be calculated through s parameters and through simulations as explained here
Falstad Simulations
https://tinyurl.com/29n95sl8: Lumped Element Model showing Standing Waves
*Wavelength has to be multiple of transmission line length, so frequency in this case has to be a multiply of 10.
https://tinyurl.com24httn2v: Lumped Element Model showing lossless Transmission line
*For the lumped element model, there are slight inaccuracies since there are only 32 elements, not nearly as high as the transmission line package.
Notice the time delay for the transmission line, ~32ms, is consistent with Heaviside’s findings, as since our values for L and C are 1H/m and 1uF/m respectively, the wave speed should be around 1000m/s. Since the line is 32 meters or lumped segments long, the time delay should be 32ms, supporting the Telegrapher’s equations.
XIX. On the extra current – Oliver Heaviside
III. On the theory of the electric telegraph – William Thomson
Electrical papers : Heaviside, Oliver, 1850-1925 : Volume II
On Heaviside’s contributions to transmission line theory: waves, diffusion and energy flux