Gaussian v. SI Units
For the purposes of this experiment, we will be using Gaussian Units, not SI (Système International) Units; there are several important distinctions between Gaussian and SI Units which helped us to make this decision.
What is a B-H curve?
A B-H curve, or a magnetic hysteresis curve, maps the relationship between the magnetic field strength (H) and the magnetic flux density (B). Such a curve makes evident the lasting induced magnetization of certain materials. The curves are created by measuring the magnetic flux density of a material while changing the magnetic field that material is in. The result is lasting magnetization of the material, which is evident due to a remaining magnetic flux density of the material called the remanence (this will be discussed more below).
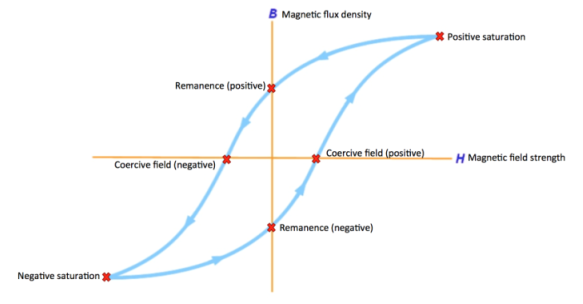
This graph is more specifically called a hysteresis loop because it consists of two magnetization curves that form a closed loop. There are two curves because we utilize an AC current source, so the magnetic field and flux density flip sign, which creates one positive and one negative curve.
B-H curves are useful in determining several important magnetic properties of a magnetic or magnetizable material.
B, H, and M
These three variables all seem very similar, but there are in fact important distinctions between them. B is the magnetic flux density, while H is the magnetic field strength, and M is the magnetization. You can think of H being the auxiliary field, or the magnetic field in a vacuum, while M is the induced field. Then B is the total field, which is a summation of the auxiliary field and the induced field. Though sometimes confusing, these three variables are necessary because often magnetic fields that have been generated pass through materials which themselves contribute magnetic fields, so uncertainties arise about what part of the final magnetic field comes from the original field and what part comes from the material the original field passed through. These ambiguities can be cleared up by describing the original auxiliary field as H, the internal field of the material as M, and the final field as B.
edit:
(((((Previously, the relative permeability, symbol μr was defined as the ratio of the absolute permeability μ and the permeability of free space μo (a vacuum) and this was given as a constant. However, the relationship between the flux density, B and the magnetic field strength, H can be defined by the fact that the relative permeability, μr is not a constant but a function of the magnetic field intensity thereby giving magnetic flux density as: B = μ H.))))
