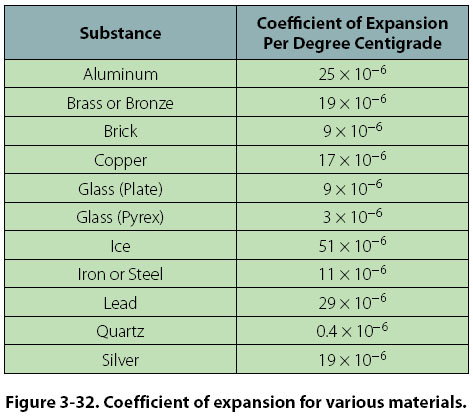
Thermal Expansion
———————————————-
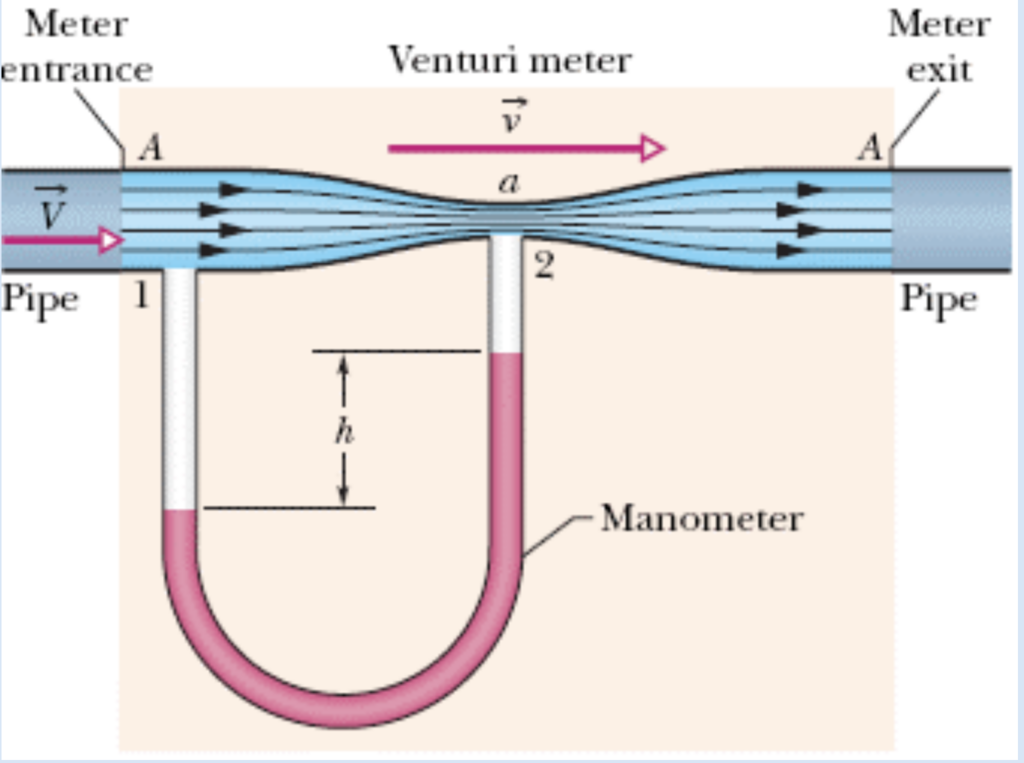
Venturi Effect
Poincaré was an influential French philosopher of science and mathematics, as well as a distinguished scientist and mathematician. In the foundations of mathematics he argued for conventionalism, against formalism, against logicism, and against Cantor’s treating his new infinite sets as being independent of human thinking. Poincaré stressed the essential role of intuition in a proper constructive foundation for mathematics. He believed that logic was a system of analytic truths, whereas arithmetic was synthetic and a priori, in Kant‘s sense of these terms. Mathematicians can use the methods of logic to check a proof, but they must use intuition to create a proof, he believed.
He maintained that non-Euclidean geometries are just as legitimate as Euclidean geometry, because all geometries are conventions or “disguised” definitions. Although all geometries are about physical space, a choice of one geometry over others is a matter of economy and simplicity, not a matter of finding the true one among the false ones.
For Poincaré, the aim of science is prediction rather than, say, explanation. Although every scientific theory has its own language or syntax, which is chosen by convention, it is not a matter of convention whether scientific predictions agree with the facts. For example, it is a matter of convention whether to define gravitation as following Newton’s theory of gravitation, but it is not a matter of convention as to whether gravitation is a force that acts on celestial bodies, or is the only force that does so. So, Poincaré believed that scientific laws are conventions but not arbitrary conventions.
Poincaré had an especially interesting view of scientific induction. Laws, he said, are not direct generalizations of experience; they aren’t mere summaries of the points on the graph. Rather, the scientist declares the law to be some interpolated curve that is more or less smooth and so will miss some of those points. Thus a scientific theory is not directly falsifiable by the data of experience; instead, the falsification process is more indirect.